Plaça de la Geometria

La plaça de la Geometria es troba situada, al nord-est de Borrassà, davant de l’escola d’Infantil i Primària Sant Andreu. El disseny d’aquest espai públic és obra de l’arquitecte municipal, Ferran Aizpun de la Escosura, per encàrrec de l’Ajuntament. A l'hora d’idear la nova plaça, l’arquitecte va tenir en compte l’equipament docent amb el que estaria enfrontat i això el va portar a concebre-la com un lloc lúdic i, a la vegada, educatiu, on a partir de figures geomètriques, representades als paviments, es pogués entendre la geometria d’una forma senzilla i lúdica.
L’indret permet afrontar una matèria considerada difícil com són les matemàtiques des d’una òptica més propera en veure les aplicacions que té a la vida real, cosa que es pot fer a partir dels jocs que s’han dissenyat en diversos plafons i s’han col·locat a la plaça.
L’actuació està basada en el tractament del paviment i la jardineria segons un llenguatge geomètric simple. S’hi ha dissenyat una successió de diverses peces de paviment que reprodueixen formes geomètriques pures: triangle, quadrat, circumferència, pentàgon, pentalfa –figura en forma d’estrella pentagonal- i rectangle auri o d’or –rectangle harmoniós en el que el seu costat llarg és 1.618 vegades més gran que el costat curt-, i les seves diagonals, segments i proporcions, que es combinen amb diferents espais d’estada i joc.
Les peces són fetes de diferents colors i materials reprodueixen lleis geomètriques simples i delimiten diversos àmbits d’utilització que s’han combinat amb la vegetació que ocupa part de l’espai. La proximitat de l’escola dóna suport a l’esperit didàctic d’aquesta plaça on s’hi combinen activitats lúdiques i de joc amb els elements didàctics que hi ha i les zones destinades a estada.
La plaça de la Geometria posa eines a l’aprenentatge i l’experimentació, fora de les aules, de les lleis de la geometria, que es troben constantment en el món quotidià que ens envolta. A la vegada i de forma natural fa que aquesta disciplina sigui més propera. Així, combinant l’aprenentatge amb el joc es contribueix a fer comprendre i veure a la vida real l’aplicació d’unes lleis i d’unes fórmules que és més complicat de veure a a través de l’ensenyament que es fa dins les aules.
ELEMENTS I FIGURES REPRESENTATS
El punt i la línia. S’hi representen simbolitzats per la columna de l’enllumenat que representa el punt en planta i la línia en altura. El seguit de xiprers alineats, considerats com una idealització de punts gegants, dóna com a resultat línies vegetals en planta, i la seva projecció en altura configura la creació de plans octogonals, és a dir, que formen angles rectes, al terra.
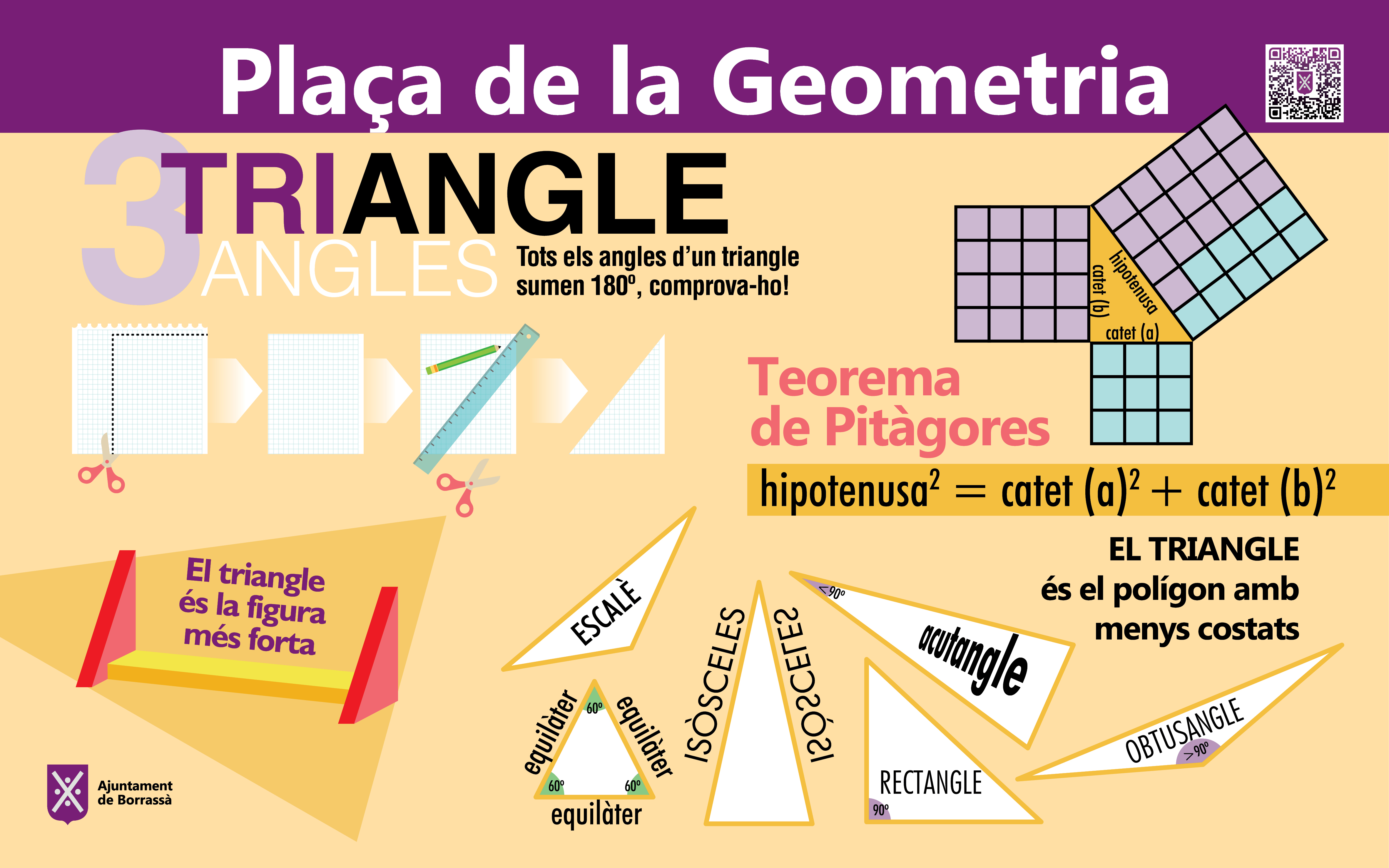
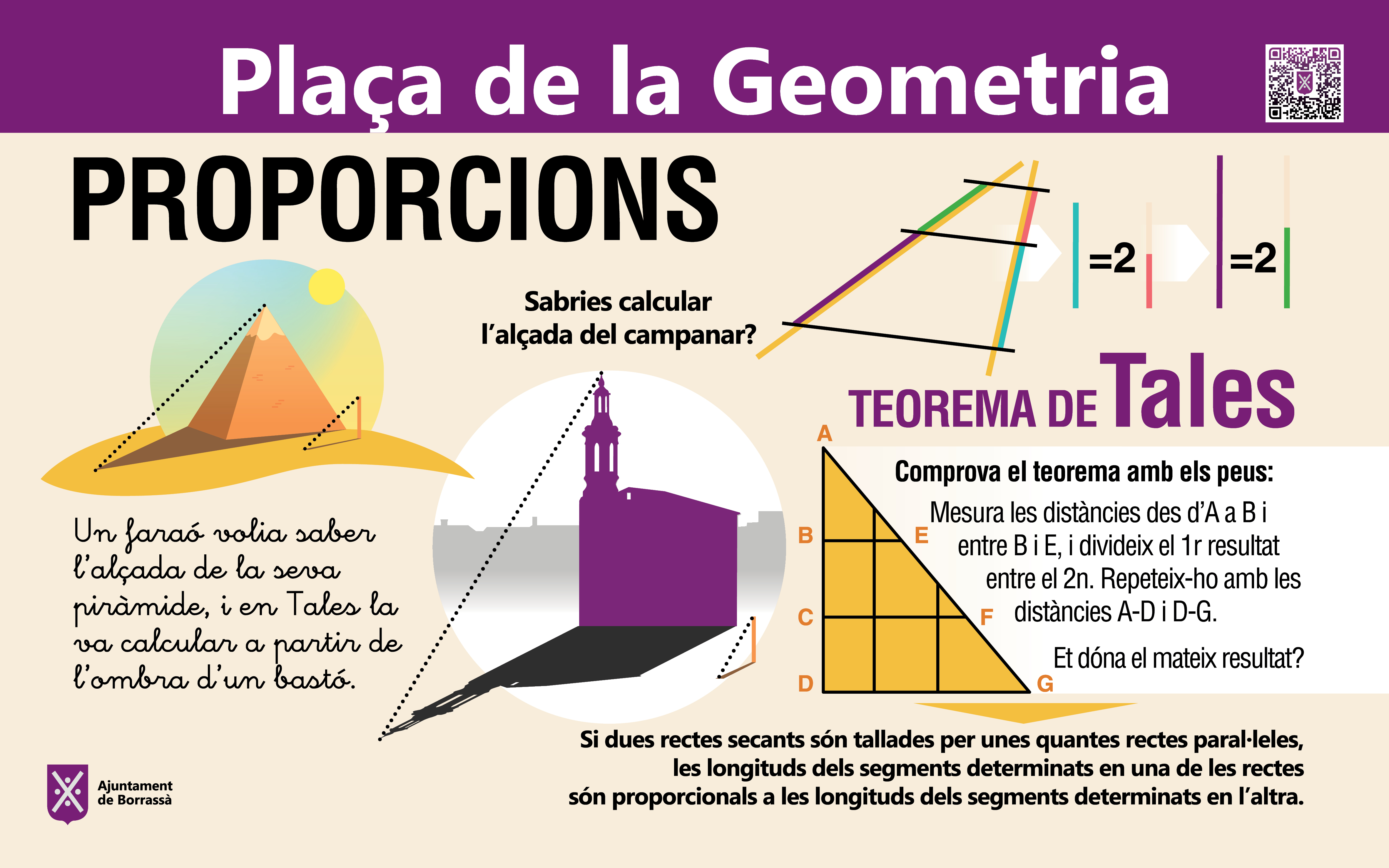
Un triangle escalè. A partir de la seva diagonal genera dos triangles rectangles, on queda reflectit el teorema de Tales (si dues rectes concurrents són tallades per un sistema de paral·leles, els segments determinats a les rectes concurrents són proporcionals). Es pot experimentar la demostració del teorema de Pitàgores (el quadrat de la hipotenusa és la suma dels quadrats dels catets), així com recorre angles interiors, medianes, mediatrius (lloc geomètric dels punts del pla que equidisten dels dos extrems d’un segment) i bisectrius (lloc geomètric dels punts que equidisten dels costats d’un angle, el qual divideix, per tant, en dos angles iguals).
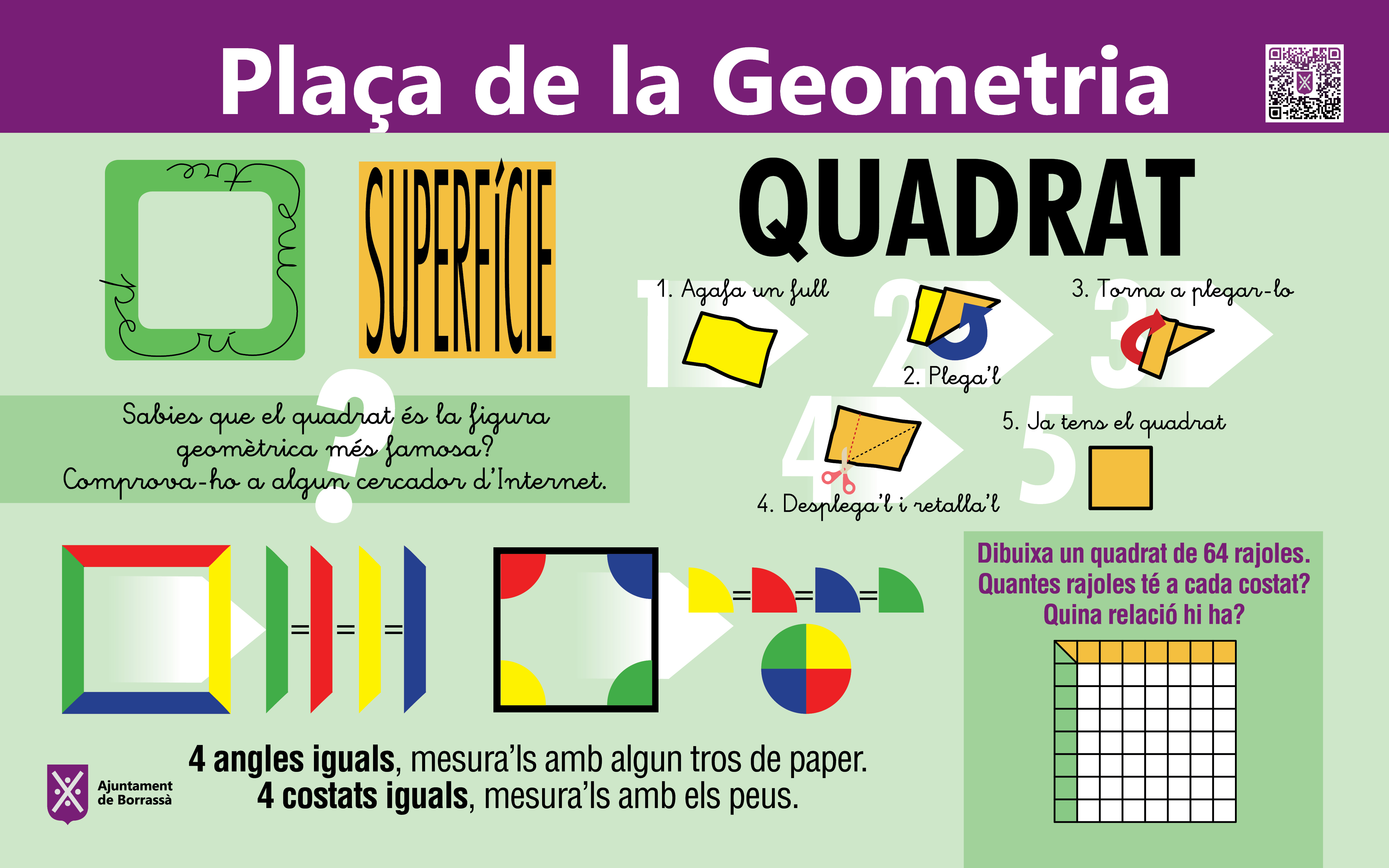
El quadrat. Format per petits quadrats, fets amb peces de paviment, amb un altre menor recolzat a la seva diagonal permet conèixer la seva geometria i, novament les proporcions de Tales i les relacions de superfície. Es pot constatar que les dues diagonals que el creuen són iguals i es troben al mig de la figura i que la longitud d’una diagonal és l’arrel quadrada de la longitud d’un costat (constant de Pitàgores).
El rectangle auri o rectangle d’or. A partir d’un quadrat i amb un compàs es pot construir un rectangle d’or: punxant al centre d’un dels costats i obrint fins a un dels dos angles oposats, només cal baixar l’arc fins a la prolongació del costat on s’ha punxat. Una de les propietats del rectangle auri és que el rectangle resultant de l’eliminació del quadrat de costat b que el pot generar (vegeu la figura), també és d’or.
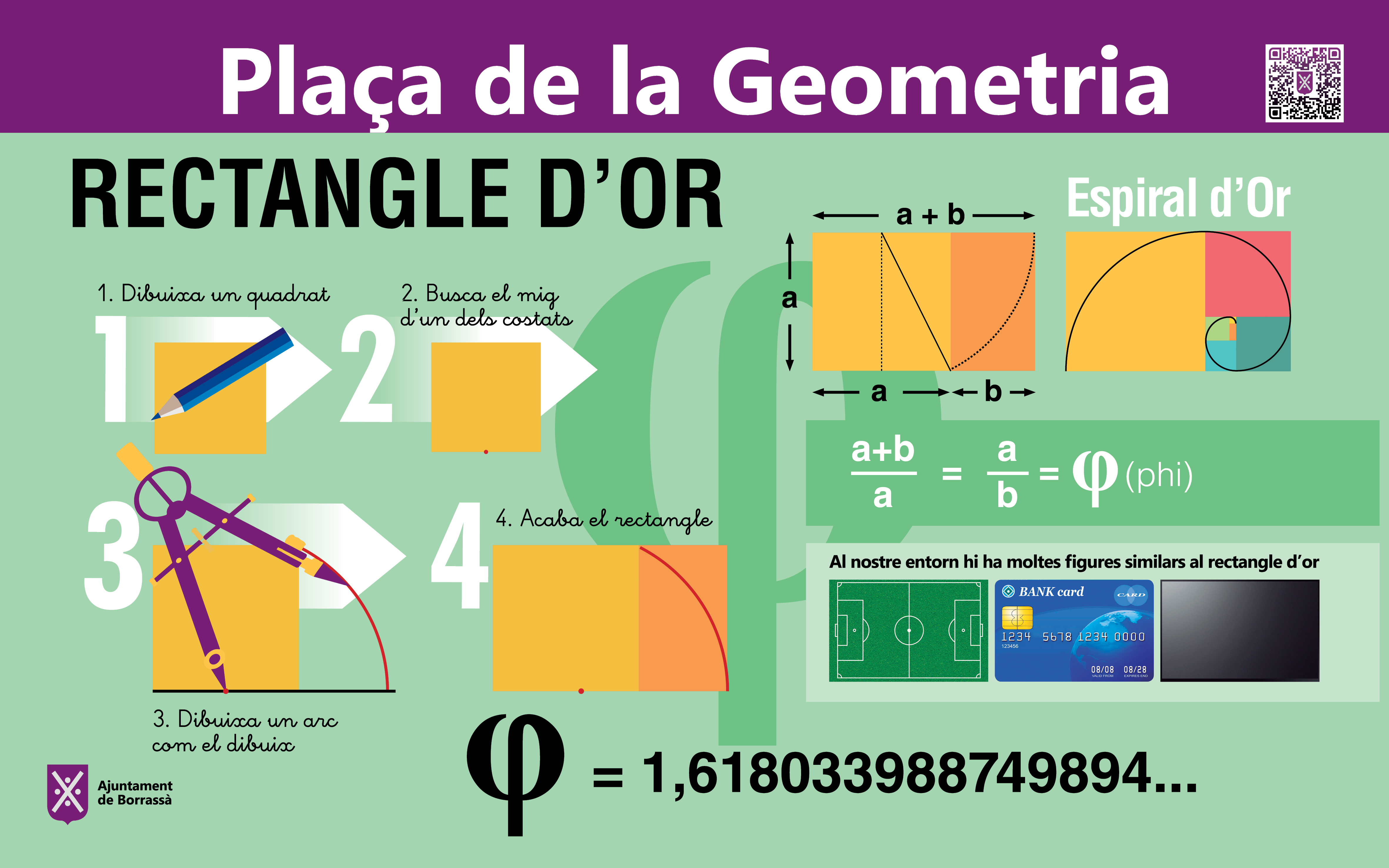
L’any 1509, Luca Pacioli publicà Divina Proportione, on a més de tractar sobre les curiositats matemàtiques del nombre d'or, també parlava del seu ús en l'arquitectura. Això va propiciar l'acceptació de la idea que molts artistes del Renaixement introduïen la raó àuria en els seus dissenys. Un bon exemple d'aquests mites es troba en les pintures de Leonardo da Vinci, on, de la mateixa manera que en el Partenó, s’hi poden trobar relacions àuries, encara que no hi ha proves fefaents que confirmin que fossin introduïdes expressament per l’autor.
En el segle XX, l'arquitecte suís Le Corbusier va publicar Le Modulor, on tractava, entre d'altres amb la raó àuria en l'arquitectura i sobretot en l'urbanisme.
La raó àuria s’ha fet servir en construccions més recents: escales, edificis i d'altres, com per exemple en la mida estàndard de carnets i targetes de crèdit que s'aproximen a rectangles d'or. Potser l'edifici més emblemàtic és la seu de l'ONU a Nova York, un gran prisma amb una de les seves cares en forma de rectangle d'or.
També ha estat usada en música tant per la durada de les notes, com van fer els compositors hongarès Béla Bartók i francès Olivier Messiaen, com per l'organització de les parts d'una peça, per exemple en alguna obra del compositor mexicà Silvestre Revueltas.
A més de raons d'or se’n poden trobar en la ramificació de determinades plantes o en la disposició dels pètals de les dàlies i altres flors. I d’espirals i angles d'or n’hi ha en les pinyes d'un pi.
El pentàgon i el pentalfa regulars. El pentàgon regular i les seves diagonals, que formen un pentalfa (o pentacle), amaguen unes quantes propietats relacionades amb la raó àuria. Per tractar-se de pentàgons regulars, s'identifiquen deu angles de 108º, cinc en el pentàgon exterior i cinc més en el format en l'interior. A partir d'aquests deu angles se’n poden trobar cinc més també de 108º (per angles oposats pel vèrtex) i deu angles de 72º (per angles suplementaris. D'aquesta manera, s'identifiquen cinc triangles d'or, que són els que formen les puntes del pentacle. També s'hi identifiquen quinze triangles d'argent (de dues mides diferents). Només hi ha doncs tres tipus d'angles: de 36º, 72º (el doble de 36º) i 108º (el triple).

Pel què fa a longitud dels segments, s'observa que només n'hi ha de quatre longituds diferents, però totes en relació àuria amb alguna altra. Per demostrar cadascuna d'aquestes relacions, només cal trobar un triangle d'or o d'argent format per costats amb les longituds corresponents. Els triangles són efectivament d'or o d'argent perquè ho corroboren els seus angles i la relació és àuria per definició de triangle d'or o d'argent.
El cercle i la circumferència. Permeten apreciar com un cercle és l'àrea del pla delimitada per una circumferència. També permeten constatar la inscripció de figures, com en aquest cas el pentàgon i el pentalfa regulars.
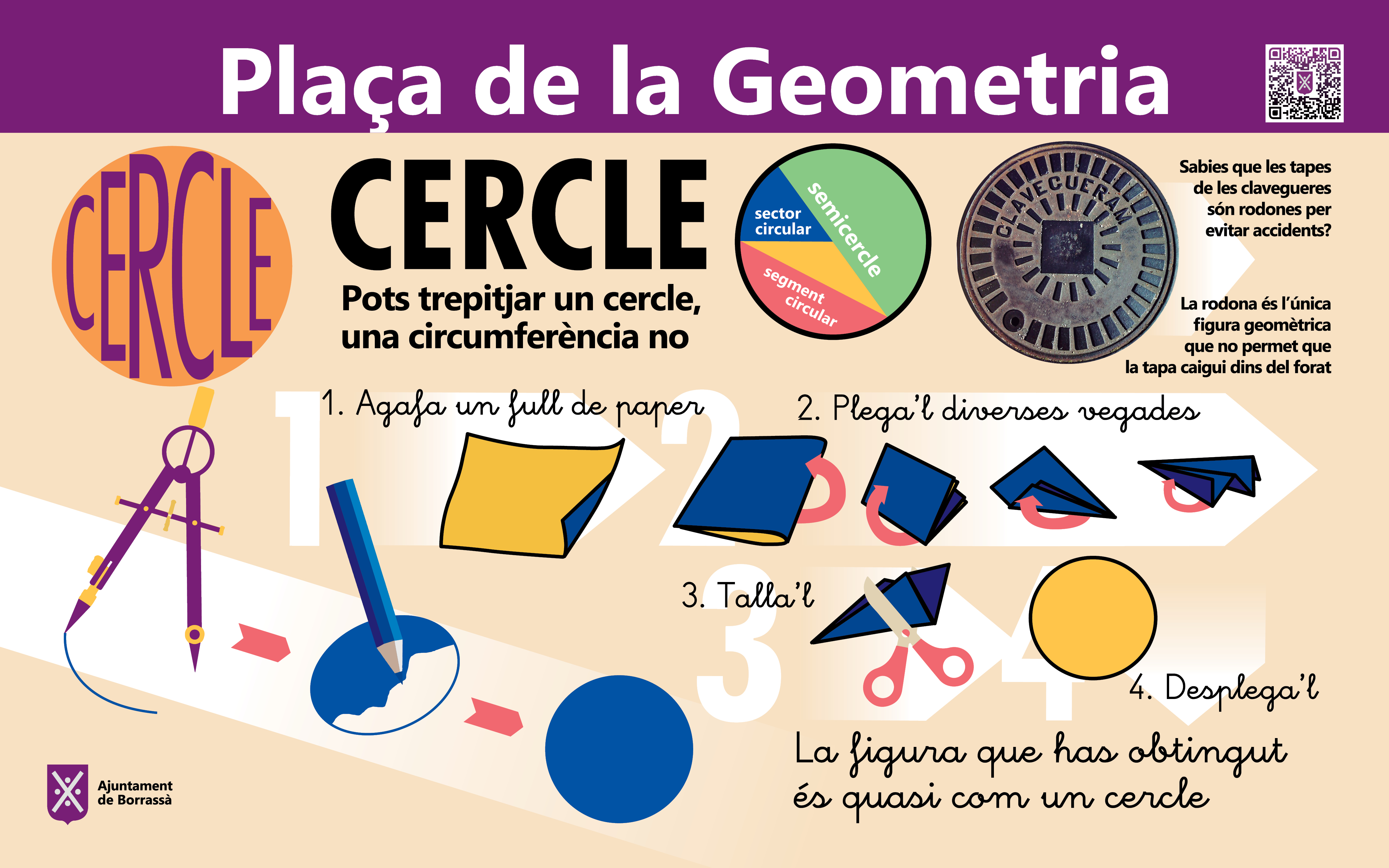

PLAFONS DE JOCS EDUCATIUS
El disseny de la plaça es completa amb nou plafons didàctics on s’hi reprodueixen diversos jocs i activitats que permeten posar a la pràctica amb elements reals les fórmules i proporcions geomètriques.
Un fa referència al concepte de geometria i a l’escala i on hi consta dibuixada la plaça; un altre a les proporcions de Tales on es donen pautes per calcular, per exemple, l’alçada del campanar de Borrassà fent servir aquest teorema; el tercer explica com es poden calcular les superfícies i en els altres sis s’hi han dissenyat activitats per fer càlculs amb el triangle, el cercle, la circumferència, el quadrat, el rectangle d’or i el pentàgon.
SIMBOLOGIA D’ALGUNES DE LES FIGURES REPRESENTADES
Aquestes figures geomètriques també donen peu a l’anàlisi de la seva simbologia, present al llarg de la història del coneixement i de l’humanisme.
QUADRAT
Durant el cristianisme el quadrat és una figura central. Representa la Terra i, per tant. també a l'home. L'origen d'aquesta associació s’inclou en una descripció del món que es troba al Gènesi.
TRIANGLE
El triangle representa l'estabilitat i la simplicitat, perquè tota figura es pot descompondre en triangles i qualsevol cos pot sostenir-se sobre tres punts de recolzament ben situats. Per això, es troba en la base de les construccions tradicionals (cabana, tipi...) i ha estat àmpliament adoptat pels arquitectes: és el perfil de les piràmides egípcies però, també, el de les teulades, dels campanars, etc.
El triangle amb la base a sota simbolitza Déu (per la doctrina de la trinitat al cristianisme). En aquest cas, a vegades amb un ull al mig, volent significar que Déu ho veu tot. Aquest símbol és igualment utilitzat per la francmaçoneria.
També era l'antic jeroglífic hittita per indicar "ciutat".
Els senyals de trànsit indicant perill o atenció tenen aquesta forma, així com el símbol de Protecció Civil.
Si, el triangle, està invertit s'associa a la dona, per la forma del pubis. Durant el nazisme, els homosexuals havien de portar un triangle invertit de color rosa. A més, és la forma del senyal de trànsit de "cediu el pas".
Com a punta d'una fletxa, significa la direcció. Quan la punta mira cap a la dreta, apareix com a representació gràfica de "play" (posar en marxa) en els aparells musicals i informàtics. Si està duplicat, indica avançament de pista o cançó.
Dos triangles superposats al revés, com en l'estrella de David, simbolitzen la noció d'harmonia i d'equilibri perfecte.
PENTÀGON
Alguns creuen que el pentàgon va ser l'escollit per Pitàgores per a la germandat que creà i presidí: els pitagòrics, per les seves diagonals, que formen un pentalfa (o pentacle) i amaguen unes quantes propietats relacionades amb la raó àuria.
El pentagrama pren la seva simbologia del número cinc. En moltes tradicions fou pres com la clau que obre la via a “l’Alta Ciència” i com a signe de reconeixement i poder. Representa el microcosmos (home), i està en contraposició amb l’estel de sis puntes (segell de Salomó), el qual representa al macrocosmos.
El Pentagrammon era pels pitagòrics un dels símbols més poderosos, ja que representava el coneixement. El feien servir al final dels seus escrits com a fórmula de salutació i el seu significat era: d’acord.
En general, el Pentagrama cap amunt es considera actiu, i passiu quan esta invertit; però en la maçoneria, com a gremi tradicional de constructors, està associat fonamentalment a les proporcions i, en concret, al Número d’Or. La proporció àuria permet construir el pentagrama que, per a l’iniciat, no és sinó la realització efectiva de la seva iniciació als Petits Misteris, realització que el converteix en Home Universal.
CITACIONS
La plaça de la Geometria també ha estat citada en aquest article, titulat "Interpretació geomètrica de l'emplaçament del monestir de Sant Pere de Rodes" de l'arquitecte municipal, Ferran Aizpun, que s'ha publicat a l'últim volum dels Annals de l'Institut d'Estudis Empordanesos.
VÍDEO fet amb un dron per Empordà Televisió. S'ha penjat al canal de youtube Borrassà TV


